Башорг такой башорг
flapenguin: Знаешь, что у моей племянницы написано в учебнике по геометрии?
flapenguin: Треугольник называется прямоугольным, если _хотя бы один_ из углов равен 90 градусам.
flapenguin: Хотя бы один бл#дь. Fuck you, Pythagoras.
На Башорге, как обычно, такие математики и профессионалы…

Нужно было уточнить что «учебник по эвклидовой геометрии в 3хмерном пространстве»
Имел в виду в 2х мерном пространстве )
Я, прочитав эту цитату сегодня утром, тоже понегодовал. :-)
К сожалению, качество образования сейчас — хуже некуда. Страшно представить, что вырастет из поколения «четырёх предметов в неделю».
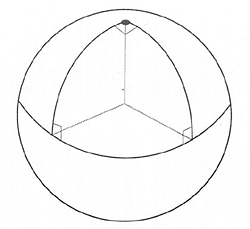
Так вон какой сферический треугольник в вакууме.
Комментарий для dinoel:
Я понимаю, только в цитате этого нет. И не факт, что в учебнике имеется ввиду фигура на евклидовой плоскости.
Комментарий для Евгения Степанищева:
Треугольник — часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки. (вики)
Является ли поверхность сферы плоскостью?
Комментарий для Александр:
Да. http://ru.wikipedia.org/wiki/%D0%A1%D1%84%D0%B5%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F
поверхность сферы является выпуклостью, а не плоскостью, так как не плоская!
Комментарий для nudnik.ru:
Скажи это Камилю Фламмариону.
Хотя бы первого апреля можно и не занудствовать ;)
Комментарий для Евгения Степанищева:
то есть любой девушке можно сказать, что ее грудь плоская?
Комментарий для isk.livejournal.com:
Ты же понимаешь, что однокоренные слова не обязательно сходны по значению? Или ты считаешь, что корнеплод это такая морфема?
Основу аудитории bash.org.ru составляют -малолетние-д- школьники и студенты. Для этой социальной группы вполне естественно лезть опрометь, не удосужившись разобраться в предмете, чуть только видят что-то, что по их мнению является бредом или маразмом. Чего стоит одна только история о том, как молодой человек насмехался над задачкой по информатике младшей сестры, ответ к которой составлял 5,6 бита! Такого рода истории действительно смешны, только невежественные люди смеются над предметом своего невежества, тогда как люди знающие смеются над рассказчиком.
Комментарий для besisland.name:
Ага. Школьники и... bolk.
Мммм... Баг што ли?
Комментарий для shcoder.by:
И я, например. Вы знаете лексическое значение слова «основу»?
with {школьный учебник по геометрии} do
..
Вообще-то даже на плоскости эта формулировка математически верна. Потому не понимаю, о чём спорить
Треугольник называется прямоугольным, если _хотя бы один_ из углов равен 90 градусам.
Всё верно. «Хотя бы один», а не «только один».
Кто негодовал — слили бы античным грекам в диспуте:)
В цитате есть чёткое указание на школьный учебник геометрии, так что мимо.
P.S. Представляете, в школьном курсе и параллельные прямые не пересекаются, вот ужас-то?
Комментарий для serge-matveev.livejournal.com:
Параллельные прямые не пересекаются ни в одном курсе геометрии просто по определению.
на самом деле чуть менее, чем все цитаты башорга — выдуманы.
Комментарий для zg.livejournal.com:
Вот та же мысль возникла. Как-то не верится, что это определение действительно записано в каком-то учебнике.
Комментарий для serge-matveev.livejournal.com:
Я отчётливо помню, что уже в школе видел вот эту картинку с треугольником на сфере. Так что не мимо. А учился я до 9-го класса (потом в техникум пошёл).
Комментарий для Евгения Степанищева:
Видеть этот рисунок ты мог и не в школьном учебнике. А в стандартной школьной программе изучают только евклидову геометрию.
Комментарий для dionys.myopenid.com:
И не рассказывают, что бывает другая?
Комментарий для Евгения Степанищева:
По идее в введении в предмет должны сказать примерно так: этот учебник — о геометрии на плоскости, о планиметрии. Приняты такие-то аксиомы (и эти аксиомы не обязаны работать на сфере, например). Позднее в курсе мы так же рассмотрим стереометрию, геометрию 3-мерного пространства.
Отметим, что участки земной поверхности меньше 100 км можно рассматривать как плоские. Поэтому землемерная деятельность, которая была важна для древних греков развивалась на основе геометрии плоскости.. В дальнейшем в этом учебнике мы говорим именно о планиметрии — и все.
Ну по простому — в первой главе with (геометрия на плоскости)...
Не было никакой сферы в школе O_o. Это школа же.
Комментарий для gogis:
И что, что школа. В школе трёхмерные объекты не проходят что ли?
Комментарий для Евгения Степанищева:
Да, есть стереометрия, 10-11 класс. Но там тоже всё эвклидово, нет треугольников на сферической поверхности. Есть трехмерные координаты, объёмы фигур, площади поверхностей, проекции трехмерных фигур на плоскость, сечения всяких пирамид и шаров плоскостями.
Скачал учебник Погорелова, 7-11 классы, не помню уж точно, но вроде бы мы учились по такому: http://ksim.ru/tmp/Pogorelov_7-11.djvu (3Mb)
Комментарий для maxim-zotov:
Я сейчас в Турции, не могу посмотреть, большой файл. Что там написано-то?
В любом случае, была неевклидова геометрия или нет, а определение прямоугольного треугольника точное.
Комментарий для Евгения Степанищева:
Про прямоугольный треугольник?
«Треугольник называется прямоугольным, если у него есть прямой угол.
Так как сумма углов треугольника равна 180°, то у прямоугольного треугольника только один прямой угол.»
Точное то оно точное, но вот вызывает лишние непонятки, вопросы и, как следствие, забивание детской головы лишней информацией. Не нужно это детям, материал нужно давать постепенно, детям нужно сначала разобраться в простой схематичной вселенной.
Например, у Погорелова тоже точное определение: «если у него есть прямой угол», но вот чудо толковой формулировки, не заострил он внимание на «хотя бы один», и определение не вызывает крамольных сферических мыслей, при этом оставаясь точным в более широком смысле.
Комментарий для maxim-zotov:
Да, хорошая формулировка, согласен.
На приведенном вверху рисунке две параллельные прямые пересекаются в зените. :-)
А есть еще и геометрия Лобачевского, модели Пуанкаре с пересекающимися параллельными.